Cet article vous réserve des surprises en utilisant vos mathématiques de niveau primaire ou secondaire… et plus ! Les sujets suivants seront abordés :
- Empiler des feuilles de papier pour atteindre le sommet de la tour Eiffel de 330 mètres de hauteur
- Plier une feuille de papier pour atteindre le sommet de la tour Eiffel de 330 mètres ou la Lune
- Impressionnant nombre
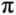(pi) - Le plus petit nombre, le plus grand nombre positif et l’infini
- Les outils de calcul à partir des années 60 jusqu’à nos jours
- Le monde des nombres complexes et imaginaires
- Épilogue
Cet article va du simple au complexe, mais c’est toujours expliqué sans prétention. Il est possible de constater que les outils permettant de manipuler les nombres ont évolué dans le temps, notamment avec nos ordinateurs personnels.
Bonne lecture !
A. Empiler des feuilles de papier pour atteindre le sommet de la tour Eiffel de 330 mètres de hauteur
Si nous utilisons une feuille de papier standard de 0,1 millimètre d’épaisseur, nous pouvons calculer combien de feuilles de papier seraient nécessaires pour atteindre le sommet de la tour Eiffel de 330 mètres de hauteur, soit :
333 000 mm divisés par 0,1 mm =
3 330 000 feuilles de papier
Il faudrait donc empiler 3,33 millions de feuilles pour atteindre le sommet de ce monument touristique.
B. Plier une feuille de papier pour atteindre le sommet de la tour Eiffel de 330 mètres ou la Lune
Chaque fois que vous pliez une feuille de papier, son épaisseur double. Si nous commençons par la feuille de papier standard de 0,1 mm d’épaisseur de l’exemple précédent, nous pouvons trouver combien de fois il faut la plier pour atteindre les 330 mètres de la tour Eiffel.
Nous utilisons la formule suivante pour trouver le nombre de pliages nécessaires représenté par la variable n :
0,1×2n = 330 000
où la hauteur est exprimée en millimètres
en réarrangeant les termes :
2n = 3 300 000
Pour résoudre cette équation, nous devons trouver n en utilisant les logarithmes :
n = log2(3 300 000) = 21,68
Donc, il faudrait plier une feuille de papier environ 22 fois pour atteindre la hauteur de la tour Eiffel.
Nous pouvons calculer combien de fois il faudrait plier une feuille de papier pour atteindre la Lune à 384 400 km de distance.
n = log2(384 400 000 000) = 31,84
où la distance est exprimée en millimètres
Avec un pliage d’environ 32 fois, on atteint donc la Lune.
Il est incroyable de voir comment de petites choses peuvent s’additionner pour atteindre mathématiquement des dimensions impressionnantes !
Toutefois, essayer d’empiler 3,33 millions de feuilles de papier ou de replier 22 fois une même feuille relève de l’impossibilité. Faites un essai avec une feuille de papier et vous constaterez une limite physique après 7 ou 8 pliages.
Atteindre la Lune en pliant du papier, c’est incroyable, mais mathématiquement calculable ! Trump pourrait parler ici d’une réalité alternative. Cela ne se fait pas, mais ça se calcule !
C. Impressionnant nombre 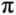(pi)
Il s’agit d’un nombre populairement connu permettant notamment de calculer l’aire ou la circonférence d’un cercle. Il est infiniment long dans sa partie décimale. Combien long ? Aussi long que vous le désirez !
Selon Microsoft Copilot, le record actuel pour le plus grand nombre de chiffres mémorisés après le point de (pi) est détenu par Rajveer Meena avec 70 000 décimales. Il a réalisé cet exploit le 21 mars 2015 à l’Université VIT à Vellore, en Inde, tout en portant un bandeau sur les yeux pendant près de 10 heures.
Cependant, Akira Haraguchi, un ingénieur japonais à la retraite, a mémorisé et récité 100 000 décimales de (pi) en 16 heures le 3 octobre 2006. Bien que ce record ne soit pas officiellement reconnu par le Guinness World Records, cela reste une prouesse impressionnante.
C’est incroyable de voir jusqu’où peut aller la mémoire humaine ! Voulez-vous exercer votre mémoire ? Les 25 premières décimales de (pi) sont : 3,1415926535897932384626433.
On se contente souvent de 3,1416. C’est fascinant de voir à quel point ce nombre irrationnel est à la fois précis et infini !
De par sa définition par rapport au cercle, (pi) se retrouve dans de nombreuses formules de trigonométrie et de géométrie, notamment celles concernant les cercles, les ellipses et les sphères. On le reconnaît également dans des formules d’autres domaines scientifiques, tels que la cosmologie, la thermodynamique, la mécanique et l’électromagnétisme.
D. Le plus petit nombre, le plus grand nombre positif et l’infini
Le nom du plus petit nombre est très connu, c’est zéro, pour 0. Il représente l’absence, le rien.
L’infini, en mathématiques, signifie un nombre plus grand que tout autre nombre. Il reste toujours indéfini et il est symbolisé par 
. Pour tout grand nombre défini, si grand soit-il, il y aura toujours un nombre plus grand !
Avant de vous parler du googolplex, il faut d’abord introduire la notion du googol, un très grand nombre défini. 1 googol est composé de 1 suivi de 100 zéros, soit 10100.
10 x 10 x 10 x 10 x 10 x 10 x 10 x 10 x 10 x 10 x 10 x 10 x 10 x 10 x 10 x 10 x 10 x 10 x 10 x 10 x 10 x 10 x 10 x 10 x 10 x 10 x 10 x 10 x 10 x 10 x 10 x 10 x 10 x 10 x 10 x 10 x 10 x 10 x 10 x 10 x 10 x 10 x 10 x 10 x 10 x 10 x 10 x 10 x 10 x 10 x 10 x 10 x 10 x 10 x 10 x 10 x 10 x 10 x 10 x 10 x 10 x 10 x 10 x 10 x 10 x 10 x 10 x 10 x 10 x 10 x 10 x 10 x 10 x 10 x 10 x 10 x 10 x 10 x 10 x 10 x 10 x 10 x 10 x 10 x 10 x 10 x 10 x 10 x 10 x 10 x 10 x 10 x 10 x 10 x 10 x 10 x 10 x 10 x 10 x 10
Le plus grand nombre connu et défini n’est pas l’infini , qui lui est indéfini, mais plutôt le googolplex, où celui-ci est 10 à la puissance de 1 googol, c’est-à-dire un nombre extrêmement grand.
En termes plus simples, un googol est déjà un nombre incroyablement grand, mais le googolplex l’est exponentiellement plus, surpassant notre compréhension des nombres. Le concept de l’infini représente une quantité indéfinie, alors que le googolplex possède une valeur définie. L’ampleur d’un googolplex aide à illustrer l’immensité des nombres.
Le terme « googolplex » a été inventé par Milton Sirotta, le neveu de neuf ans du mathématicien Edward Kasner, concepteur du nombre en 1920. C’est un nombre si grand qu’il dépasse notre capacité à le représenter physiquement ou mentalement. Il dépasse le nombre total de particules dans l’univers observable.
Lors de la fondation de la société Google, celle de notre Gmail et de notre moteur de recherche, cette entreprise avait envisagé de se nommer Googol !
E. Les outils de calcul à partir des années 60 jusqu’à nos jours
Dans les années 60 et avant, il n’y avait pas d’ordinateurs ni de calculatrices électroniques, mais simplement des petites tabulatrices généralement utilisées pour la gestion et la comptabilité. Pour les scientifiques, dont moi, comme étudiant à l’école Polytechnique de Montréal, il y avait la règle à calcul et des tables de logarithmes.
Par exemple, faire la multiplication de 12,4568 par 3,1416 avec précision de 4 chiffres après le point était une grosse tâche. Manuellement, houache ! Mais, avec la règle à calcul et les tables, on y arrivait pendant un examen !
Dans les années 70, il y avait des calculatrices électroniques pour faire autant les calculs arithmétiques de base que des calculs mathématiques plus avancés. La toute nouvelle calculatrice électronique de Texas Instrument vers 1973 coûtait 120 $. Son prix avait baissé de 25 $ six mois plus tard.
À cette époque, on venait d’emménager dans notre première maison. Ma conjointe attendait notre deuxième fils. Le budget était un peu serré et l’achat d’un tel gadget n’était pas prévu.
Une offre de la carte de crédit Shell proposait cet appareil moyennant un paiement mensuel de 10 $ pendant 12 mois ! Comme ingénieur chez IBM, la tentation fut trop forte.
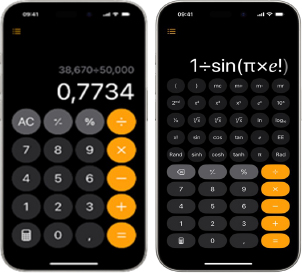De nos jours, on retrouve sur l’iPhone une calculatrice moderne avec des fonctions avancées.
Ouvrez l’application Calculatrice sur votre téléphone, puis vous pourrez effectuer l’une des opérations offertes avec des fonctions algébriques, exponentielles, logarithmiques, trigonométriques et plus. Pour utiliser la calculette scientifique, veuillez cliquer ici.
Les téléphones intelligents Samsung offrent aussi une application de calculette.
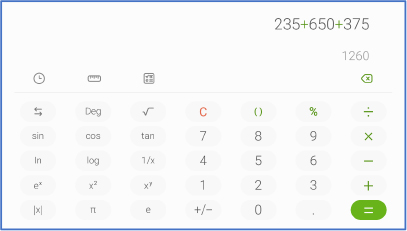
D’autres outils informatiques sur ordinateur personnel permettent de faire des calculs mathématiques avec des logiciels. Mentionnons notamment les fonctions dans Microsoft Excel ou, autrefois, dans Quattro Pro, Lotus 1-2-3 et Visicalc. Dès 1989, j’avais créé un fichier tableur pour calculer et gérer mon hypothèque bancaire.
J’ai dû me trouver un bon livre de mathématiques à la bibliothèque locale pour me remémorer les formules d’annuités. Je connaissais ma dette au cent près en tout temps et j’étais capable de modifier le tout selon les scénarios de remboursements et les variations des taux hypothécaires.
Par contre, en 2025, aucun outil n’est encore offert ou en développement pour permettre la manipulation des nombres du type Googolplex !
F. Le monde des nombres complexes et imaginaires
Les élèves du primaire apprennent que la racine carrée de -1 n’existe pas. Mais, en mathématiques de niveau collégial et universitaire, la racine carrée de – 1 est définie par
et il s’agit d’un nombre imaginaire.
On retrouve le monde des imaginaires dans divers domaines scientifiques, incluant leur utilisation dans les formules et les calculs, notamment en physique et en mathématiques.
En mathématique avancée, on définit un nombre complexe comme un nombre composé d’un nombre réel et d’un nombre imaginaire. Il y a aussi la relation entre les nombres complexes et le calcul matriciel.
Les nombres imaginaires sont une astuce mathématique étonnamment efficace pour mener des calculs. Mais, ils seraient bien plus que cela. Sans eux, la théorie quantique standard est incapable de décrire certaines expériences !
À l’université, j’adorais résoudre par la méthode des imaginaires les équations différentielles et intégrales. Pour la plupart des étudiants, c’était horrible, mais pour moi, c’était presque de la poésie ! Je me souviens de l’excellent cours sur les imaginaires donné par le professeur Henri-François Gautrin, qui devint un politicien connu comme député et ministre.
G. Épilogue
On peut toujours se questionner à savoir si les mathématiques sont une science ou même une science exacte ! Dans notre monde quotidien du réel et des calculs arithmétiques de base, c’est bien le cas.
Mais, lorsqu’on considère que les mathématiques servent à tenter de décrire les réalités très complexes de notre monde et de notre univers, alors je pense que celles-ci forment un outil de recherche assez ésotérique pour la compréhension et la maîtrise des phénomènes universels.
Nos savants prix Nobel dans tous les domaines tentent de mettre tout en équations pour expliquer et prédire ! Ils découvrent des constantes universelles, comme la vitesse de la lumière dans le vide, la constante gravitationnelle, la constante de Planck, la masse et la charge d’un électron. Les photons de lumière sont maintenant découverts, mais pas les gravitons prédits par la théorie quantique et ses équations.
Lauréat du Prix de la Banque de Suède pour ses contributions sur la théorie des jeux et de la négociation en sciences économiques ainsi que du prix Abel pour les mathématiques, John Nash eut sa vie portée au grand écran avec le film Un homme d’exception. Pour leur part, Isaac Newton, Albert Einstein et Stephen Hawking sont trois exemples de physiciens qui ont passé leur vie à tenter de mettre l’univers en équations !
Robert Lapointe
Merci Robert pour cet excellent article qui remet formidablement bien le contexte et les limites des maths!
Note : Le petit manuel de la photo avec la règle à calcul est intitulé Mathematical Tables from Handbook of Chemistry and Physics, que j’ai toujours dans ma bibliothèque personnelle depuis les années 60, contient des formules et des tables notamment les tables de logarithmes.